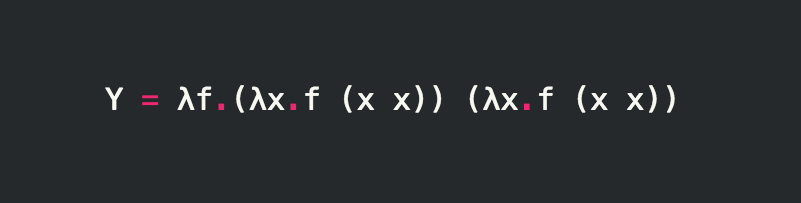That is to say c is a fixed point of the function f x if f c c. Its from a mathematical concept called fixed-point combinator.
Y Combinator The Fixed Point Combinator Function
I would like to understand how to derive FIX from first principles.
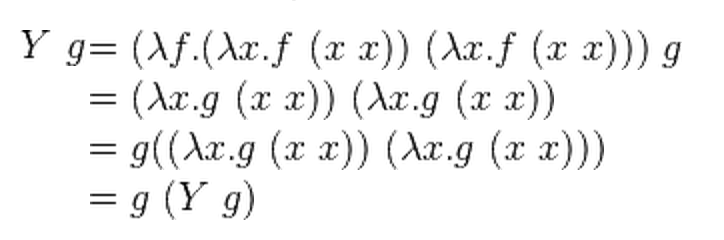
Y fixed point combinator. For sets X Y functions f. The Y combinator is a concept in functional programming borrowed from the lambda calculus. Fixed Point Operators Consider a fixed point operator Fix such that F Fix F Fix F or equivalently Fix F F Fix F Fix is a function that takes any function f an argument and then repeats the function f applied to Fix F there are many such fixed point operators The lazy Y combinator is a fixed point operator Y.
α f g g g g f g g. The solution is to eta convert f. Y f f y f f f y f f f f y f.
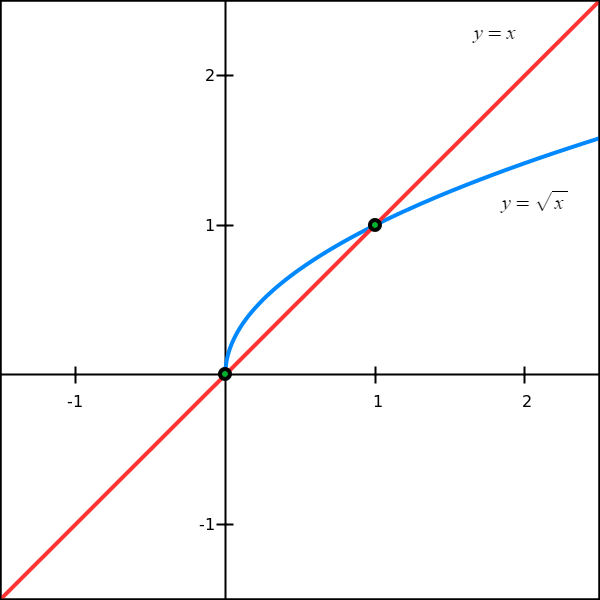
Fixed point of a function is an element of the functions domain that is mapped to itself by the function. Y f f y f for all f where y is a combinator f is function and space is function application. Fixpoint combinators are infinitely many and recursively-enumerable.
It is a fixed-point combinator. Define the stateless Y combinator and use it to compute factorials and Fibonacci numbers from other stateless functions or lambda expressions. A fixed point is a value that is unchanged by a function satisfying the equation which can be found here.
There are infinitely many fixed-point combinators and all of them are brain-wrenchingly complicated. X X Y α. A more commonly discussed.
When reducing Y f in applicative order the self application in expression f g g leads to infinite reduction which need to be blocked. Applicative order fixed point combinator Z combinator and recursion The above Y combinator does not work in C. The Y combinator is the simplest of the class of such functions called fixed-point combinators.
Y f f y f It is so named because by setting x y f it represents a solution to the fixed point equation. A combinator is a type of higher-order function that can be used to express functions without the explicit use of variables. C0x implementation of the Fixed-point Y-combinator.
If g is representable by f g then α has a fixed point. Adventures in Functional Programming. Y-combinator is a fixed-point combinator.
X X f Y Δ α X g Y. The Y Fixed-Point Combinator in PHP 01 Apr 2014. In mathematical language fGf Gf.
Fixed-point combinators are higher-order functions such that. Abstracting the recursive function. A fixed point combinator G is a higher-order function a functional in mathematical language that given a function f returns a fixed point of f.
In computer science a fixed-point combinator or fixpoint combinator is a higher-order function y that satisfies the equation. Λ Λ f Λ Δ α y Λ g Λ. X x y λx.
Y Y let g α f Δ. This expansion is recursion. The Y Combinator a function that computes fixed points for use in a recursive algorithm is a fascinating mathematical concept and its practical relevance to.
X x y I understand its purpose and I can trace the execution of its application perfectly fine. Simplest poly-variadic fixpoint combinators for mutual recursion. This expands as follows.
As a fixed point of G. The Y combinator is a famous higher order function used to implement recursion on anonymous functions ie. Now lets fit Currys Y combinator into Lawveres schema.
I tried this in Scheme and it froze my system or the case for an applicative order Y combinator. Self Application fixed points and the Y combinator. The fixed-point combinator FIX aka the Y combinator in the untyped lambda calculus λ is defined as.
A fixed point of a function f is a value that doesnt change under the application of the function f. Y combinators have the fixed point property which is formally expressed by the relation Y f f Y f. Many ways to write the fixed-point combinator in a typed practical language.
Y Combinator besides being the best investment fund is also a function of lambda calculus. One of them is. Download Y-combinator for free.
A fixed-point combinator is a magical function which takes another function as input and returns that functions fixed point as its output. X f x. This means f f f c fn c c.
The fixed point operator Y.
Dixin S Blog Lambda Calculus Via C 7 Fixed Point Combinator And Recursion
Dixin S Blog Lambda Calculus Via C 7 Fixed Point Combinator And Recursion

Fixed Point Combinators In Javascript

Y And Z Combinators In Javascript Lambda Calculus With Real Code By Enrico Piccinin The Startup Medium

Y And Z Combinators In Javascript Lambda Calculus With Real Code By Enrico Piccinin The Startup Medium

Topological Fixed Point Combinator Download Scientific Diagram

Fixed Point Illustrations Simple Examples F Int Int F N 5 N 5 Is A Unique Fixed Point F N N 2 2 N 2 And N 1 Are Both Fixed Points Ppt Download

Y And Z Combinators In Javascript Lambda Calculus With Real Code By Enrico Piccinin The Startup Medium
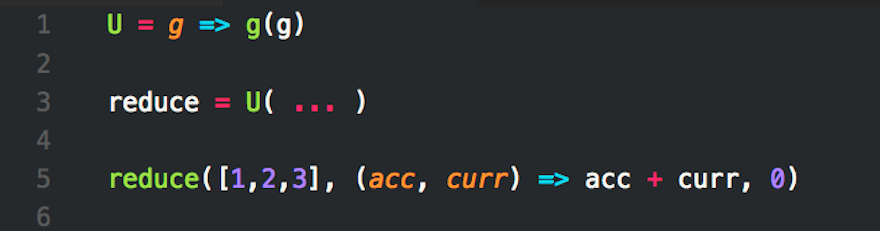
Fixed Point Combinators In Javascript

Cse 340 12 2 15 Lecture Lambda Calculus Pt 4 And Midterm 2 Review Youtube

Y And Z Combinators In Javascript Lambda Calculus With Real Code By Enrico Piccinin The Startup Medium

Ps Fixed Points 7 Fixed Points O Nierstrasz

Dixin S Blog Lambda Calculus Via C 7 Fixed Point Combinator And Recursion

Y Combinator Function What Is It Youtube
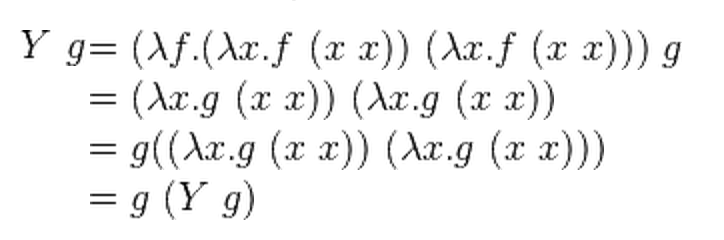
Y Combinator Beautiful Recursion By Moiz Virani Medium
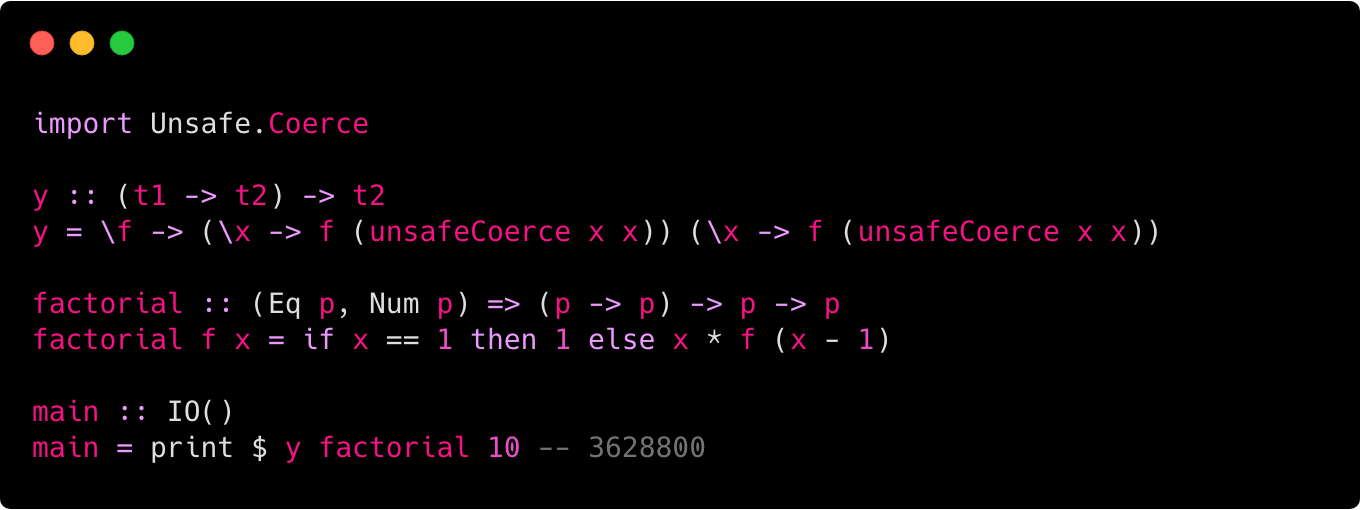
Implementing Recursion With The Y Combinator In Any Language By Michele Riva Level Up Coding

Implementing Recursion With The Y Combinator In Any Language By Michele Riva Level Up Coding